22:13
Marcelo Flora
Considere S a soma dos termos infinitos de uma PG de números estritamente positivos com razão 2 e, sendo a1 = 1.
, os termos são todos múltiplos de 2.S = (1 + 2 + 4 + 8 + 16 + 32)
Se colocarmos o 2 em evidência, teremos:
S = 1 + 2(1 + 2 + 4 + 8 + 16 + 32),
como S = (1 + 2 + 4 + 8 + 16 + 32), temos:
S = 1 + 2S
S - 2S = 1
ou seja,
S = – 1
Onde está o erro?
____________________________________________________________________________________________
Olá "Pitágoras",
Antes de analisarmos este exercício, precisamos entender o que é o infinito em matemática, e ver algumas de suas propriedades.
Gostaria de deixar bem claro que não possuo a formação necessária para demonstrar tais conceitos. Assim, dou-me ao direito de não ser muito rigoroso nesta resolução.
____________________________________________________________________________________________
Existe um paradoxo muito interessante proposto pelo matemático alemão David Hilbert (1862-1943) sobre conjuntos infinitos. É chamado “O paradoxo do Hotel de Hilbert”.
Veja:
“Considere um hotel hipotético com infinitos quartos, todos ocupados - isto é, todos os quartos contém um hóspede. Suponha que um novo hóspede chega e gostaria de se acomodar no hotel. Se o hotel tivesse apenas um número finito de quartos, então é claro que o requerimento não poderia ser cumprido, mas como o hotel possui um número infinito de quartos então se movermos o hóspede do quarto 1 para o quarto 2, o hóspede do quarto 2 para o quarto 3 e assim por diante, podemos acomodar o novo hóspede no quarto 1, que agora está vago. Por um argumento análogo é possível alocar um número infinito (contável) de novos clientes: apenas mova o hóspede do quarto 1 para o quarto 2, o hóspede do quarto 2 para o quarto 4, e em geral do quarto N para o quarto 2N, assim todos os quartos de número ímpar estarão livres para os novos hóspedes.”
____________________________________________________________________________________________
Este paradoxo nos mostra que não devemos pensar no infinito como um número real.
Ocasionalmente, considera-se ao infinito como sendo um número especial, adicionando os símbolos 
e 
ao conjunto dos números reais 
, formando assim o conjunto de números reais estendidos: 
.
e ao conjunto dos números reais , formando assim o conjunto de números reais estendidos: . Com isto, pode-se manipular o infinito como se fosse um número, porém sujeito a certas regras:
Relação de ordem: 
para qualquer número real x. 
Operações aritméticas entre infinitos:
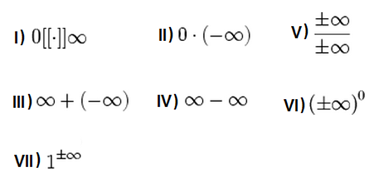Fontes: http://pt.wikipedia.org/wiki/Infinito
http://pt.wikipedia.org/wiki/Paradoxo_do_Grand_Hotel_de_Hilbert
Agora que já sabemos algumas informações sobre o infinito na matemática, vamos abordar o nosso problema.
____________________________________________________________________________________________
Podemos facilmente ver que a soma 
dos termos infinitos de uma PG de números estritamente positivos com razão 2, com 
, é igual a infinito. Portanto, temos:
dos termos infinitos de uma PG de números estritamente positivos com razão 2, com , é igual a infinito. Portanto, temos: = Desta forma, temos que tratar de um modo especial, como visto anteriormente.
Após o número 2 ser colocado em evidência, de um modo especial, como visto anteriormente. 
substitui-se no lugar da soma da PG, S.
= 1 + 2 Para ficar evidente o erro, vamos substituir
por . = 1 + 2 Para passar 2 para o outro lado da equação, teríamos que subtrair 2 de ambos os lados, o que gera uma indefinição (Veja a propriedade IV apresentada anteriormente).
para o outro lado da equação, teríamos que subtrair 2 de ambos os lados, o que gera uma indefinição (Veja a propriedade IV apresentada anteriormente). 
Assim, fica impossível prosseguir com o cálculo, tornando incorreta a resolução apresentada.
Bom, é isso. Caso alguém tenha algum comentário ou sugestão sobre este problema, ficarei muito interessado em discutí-lo.
Um abraço! E bom feriado!
Marcelo Flora
____________________________________________________________________________________________
Saiba como enviar suas dúvidas. Clique aqui!
Posted in: 
3 comentários:
Muito bom o post! Muitas vezes somos levados, pelo uso da palavra no cotidiano, a pensar que 'infinito' é uma coisa só, mas na verdade existem 'infinitos' de tamanhos diferentes.
Tudo bem Marcelo? Primeiro quero te dar os parabéns por criar um blog de matemática sem ser professor ou estudante de matemática. Com certeza o teu blog vai longe! Quanto a parceria, pode ter certeza que está 100% fechada.
Só quero pedir para você criar um banner 95x50 estático, ou 120x60. O menor será colocado na sidebar lateral, e o maior no footer do blog antes das calculadoras.
Qualquer dúvida pergunta no blog. Um abraço e bom trabalho!
Uma possível análise desse problema, mas que não parte para o tema infinito, que é tão interessante, é a seguinte:
Ao multiplicar o conjunto S por dois, a resolução proposta comete o erro de antes somar cada um dos elementos de S, para depois multiplicá-los. O fato é que, em aritmética, primeiro multiplicamos e/ou dividimos, para depois somar e/ou subtrair. A indefinição apontada pela resolução do Marcelo surge do fato de que somando todos os elementos de S não se obtém um valor real, mas sim o infinito, que não é multiplicável de forma a ter seu "valor" alterado, já que nem sequer possui um valor definido.
Postar um comentário